paxbob.blogg.se

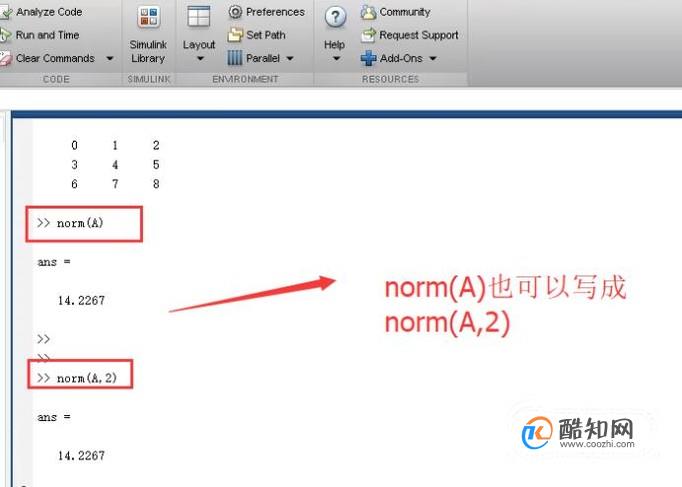
Note that norm(A), where A is an n-element vector, is the length of A. Remarks To obtain the root-mean-square (RMS) value, use norm(A)/sqrt(n). Returns sum(abs(A).^ p )^(1/ p ), for any. When A is a vector, slightly different rules apply: The Frobenius-norm of matrix A, sqrt(sum(diag(A'* A))). T he infinity norm, or largest row sum of A, max(sum(abs(A'))). The largest singular value (s ame as norm(A)). The 1-norm, or largest column sum of A, max(sum(abs((A))). Returns a different kind of norm, depending on the value of p: The Matrix 1-Norm Recall that the vector 1-norm is given by r X i n 1 1. In what follows, an 'un-designated' norm A is to be intrepreted as the 2-norm A 2. Since the 2-norm used in the majority of applications, we will adopt it as our default. Returns t he largest singular value of A, max(svd(A)). The statement norm(A) is interpreted as norm(A,2) by MatLab. The norm function calculates several different types of matrix norms: n = norm(A)

Calculate the 1-norm of the vector, which is the sum of the element magnitudes.

The 2-norm is equal to the Euclidean length of the vector. So I didn't test for the for loop and Divkar's bsxfun, but you can see that for arrays smaller than 3e4 kron is better than bsxfun, and this changes at larger arrays (ratio of <1 means kron took less time given the size of the array).Norm (MATLAB Function Reference) MATLAB Function Referenceĭescription The norm of a matrix is a scalar that gives some measure of the magnitude of the elements of the matrix. Calculate the 2-norm of a vector corresponding to the point (2,2,2) in 3-D space.

And here it is: range=3*round(logspace(1,6,200)) So I tried to check using timeit my two solutions (because they are one liners it's easy). Ok, this got me curios, as I know bsxfun starts to be less efficient for bigger array sizes. Here's a bsxfun solution (less elegant, but hopefully faster): 3 1])),3,)' A slightly shorter and vectorized way will be (if a is your matrix) : b=a-kron(a(1:3:end,:),ones(3,1))